Draw Circle Given Center and Radius
The Circle in Standard Course
A circleA circumvolve is the set up of points in a plane that lie a fixed distance from a given point, chosen the heart. is the fix of points in a plane that lie a stock-still distance, called the radiusThe fixed distance from the center of a circle to any bespeak on the circle. , from any point, called the heart. The diameterThe length of a line segment passing through the middle of a circumvolve whose endpoints are on the circle. is the length of a line segment passing through the center whose endpoints are on the circle. In add-on, a circle can exist formed by the intersection of a cone and a plane that is perpendicular to the axis of the cone:
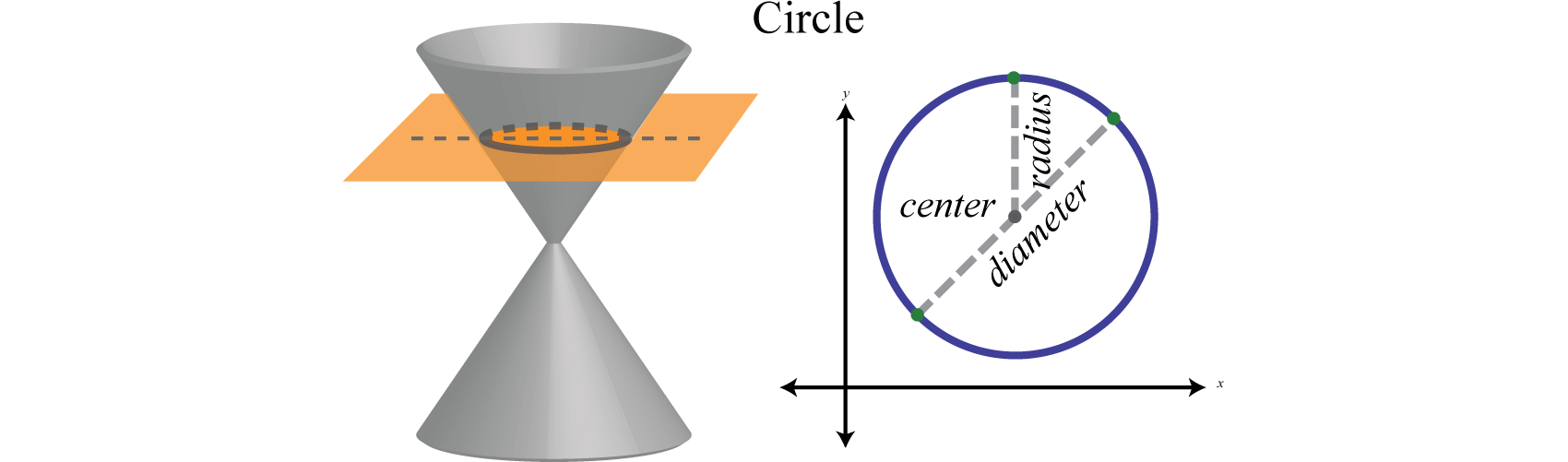
In a rectangular coordinate plane, where the center of a circumvolve with radius r is , we have

Calculate the distance between and using the distance formula,
Squaring both sides leads the states to the equation of a circle in standard formThe equation of a circumvolve written in the class where is the heart and r is the radius. ,
In this form, the middle and radius are apparent. For instance, given the equation we take,
In this instance, the middle is and More examples follow:
| Equation | Eye | Radius |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The graph of a circle is completely adamant by its center and radius.
Instance 1
Graph:
Solution:
Written in this form we can see that the center is and that the radius units. From the center mark points 4 units up and downwardly too as 4 units left and correct.
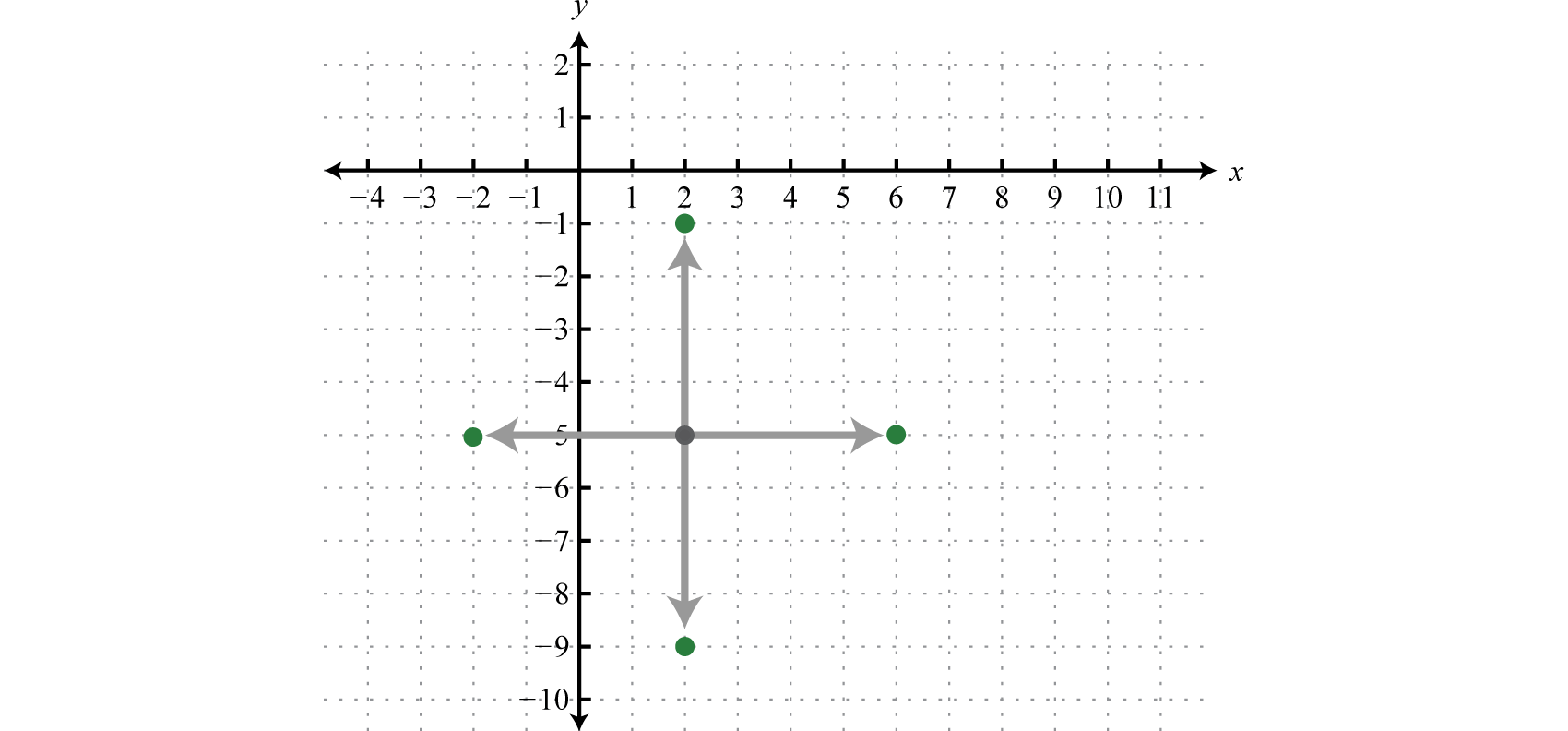
Then draw in the circumvolve through these four points.
Answer:
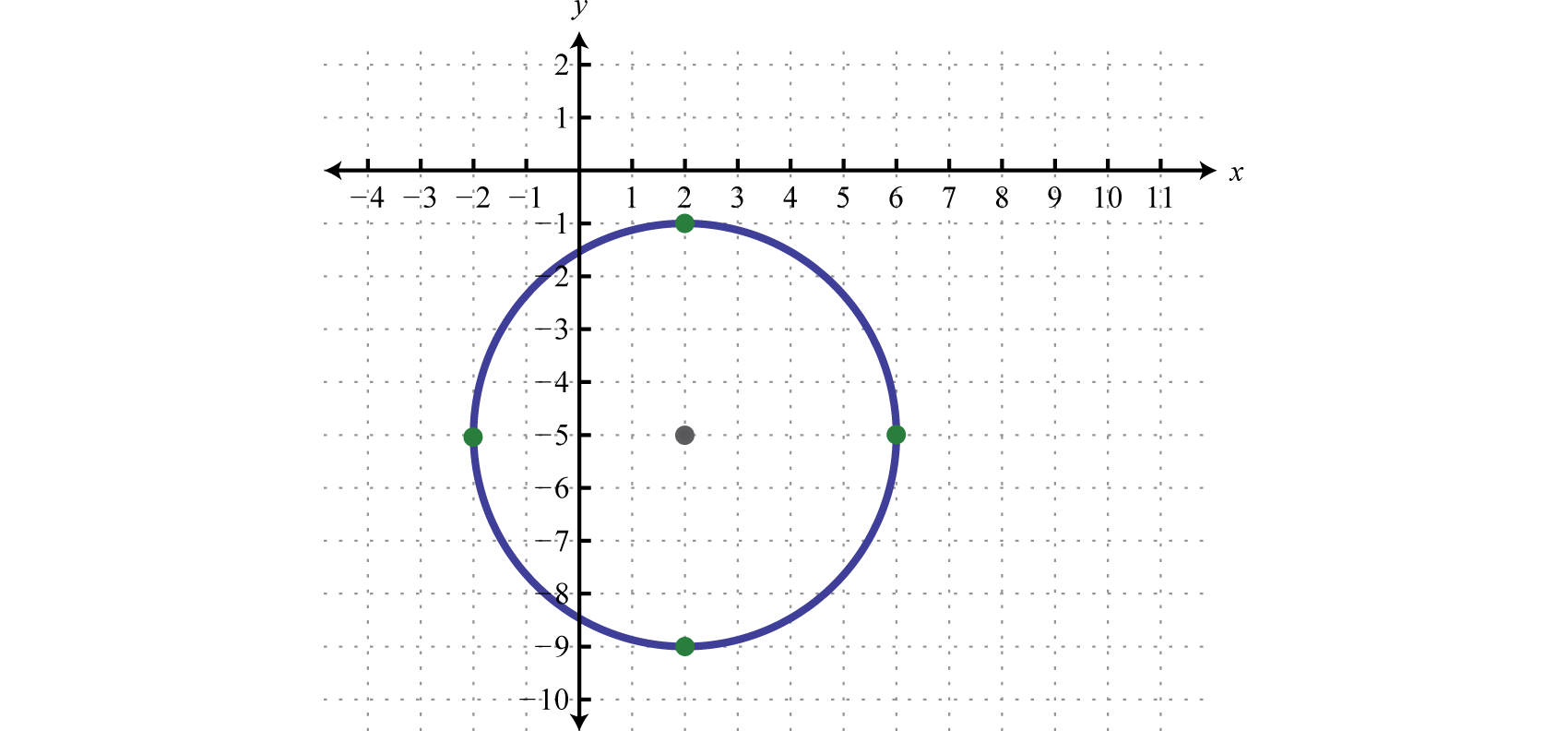
As with any graph, we are interested in finding the x- and y-intercepts.
Example 2
Find the intercepts:
Solution:
To find the y-intercepts set :
For this equation, nosotros can solve by extracting square roots.
Therefore, the y-intercepts are and To find the x-intercepts set up :
And because the solutions are complex nosotros conclude that there are no existent 10-intercepts. Notation that this does make sense given the graph.
Answer: x-intercepts: none; y-intercepts: and
Given the center and radius of a circle, we can find its equation.
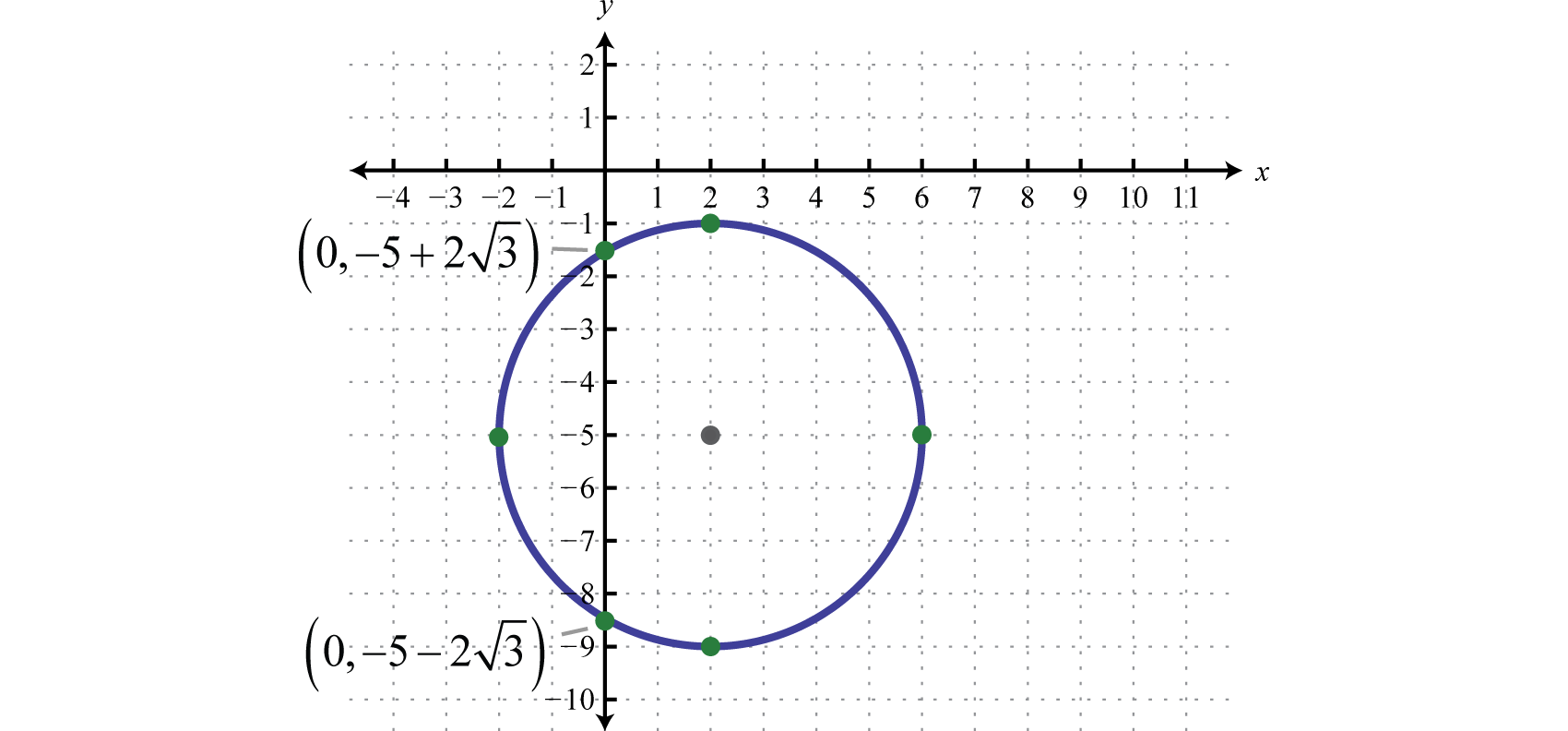
Instance 3
Graph the circle with radius units centered at Requite its equation in standard form and determine the intercepts.
Solution:
Given that the middle is and the radius is we sketch the graph equally follows:
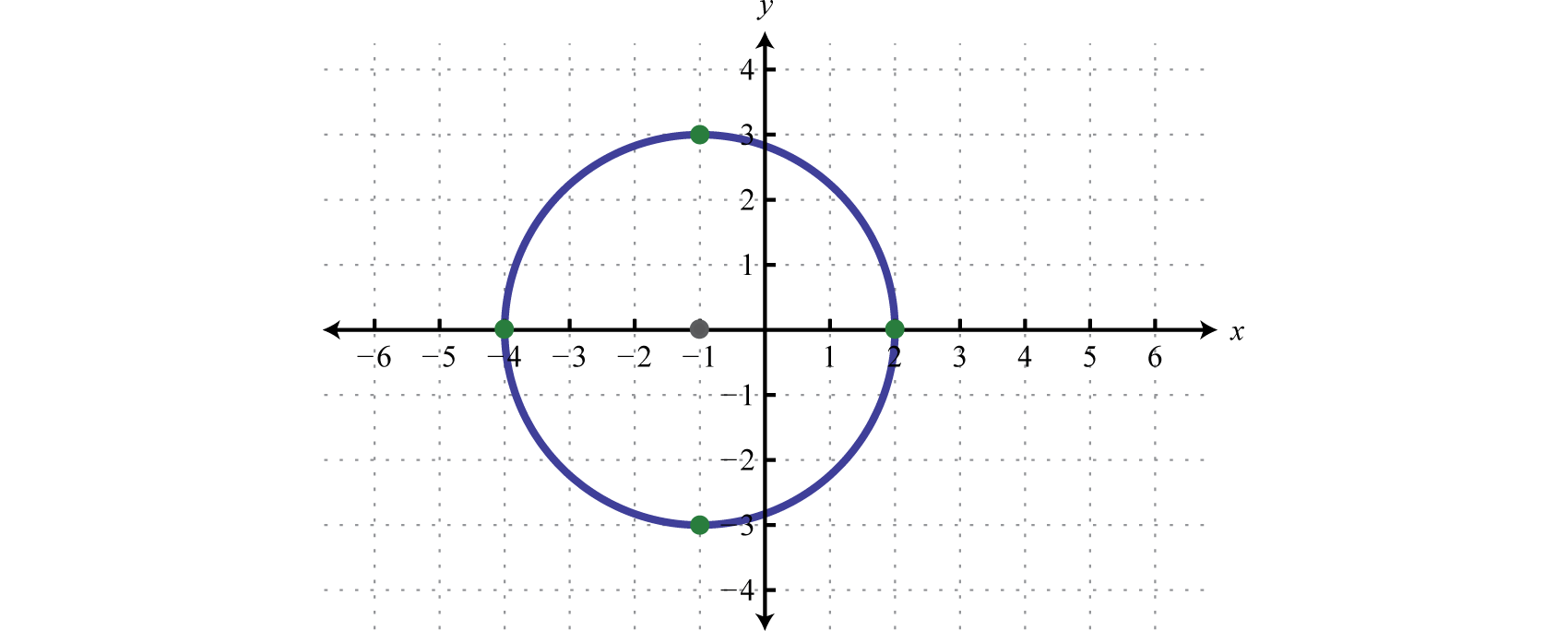
Substitute h, k, and r to notice the equation in standard form. Since and nosotros accept,
The equation of the circle is , use this to decide the y-intercepts.
Therefore, the y-intercepts are and To observe the x-intercepts algebraically, set and solve for x; this is left for the reader as an practice.

Answer: Equation: ; y-intercepts: and ; x-intercepts: and
Of particular importance is the unit circleThe circle centered at the origin with radius 1; its equation is ,
Or,
In this course, it should be clear that the center is and that the radius is i unit. Furthermore, if we solve for y we obtain ii functions:
The function defined by is the top half of the circle and the part defined past is the bottom half of the unit circle:
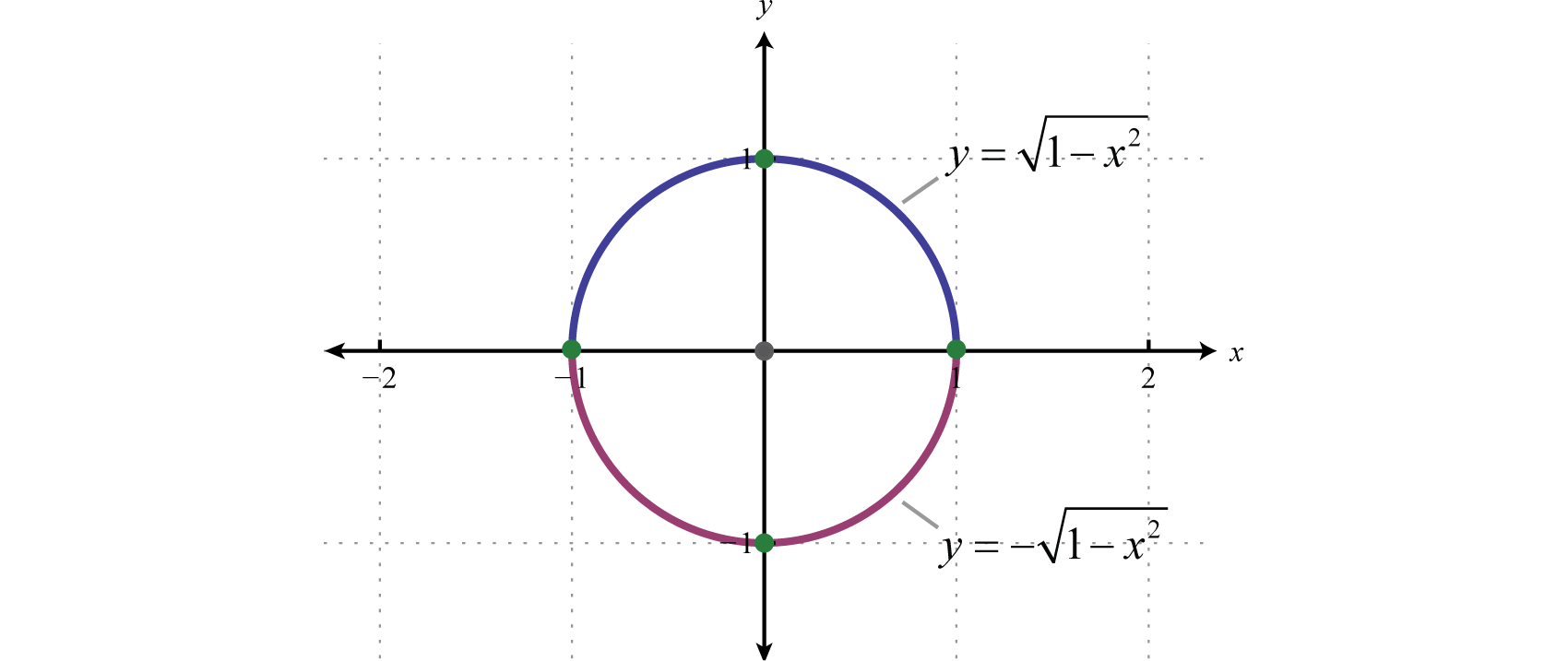
Try this! Graph and label the intercepts:
Answer:
The Circle in General Form
Nosotros have seen that the graph of a circle is completely adamant by the center and radius which tin can exist read from its equation in standard class. Withal, the equation is not always given in standard form. The equation of a circle in full general courseThe equation of a circumvolve written in the form follows:
Hither c, d, and e are existent numbers. The steps for graphing a circle given its equation in general form follow.
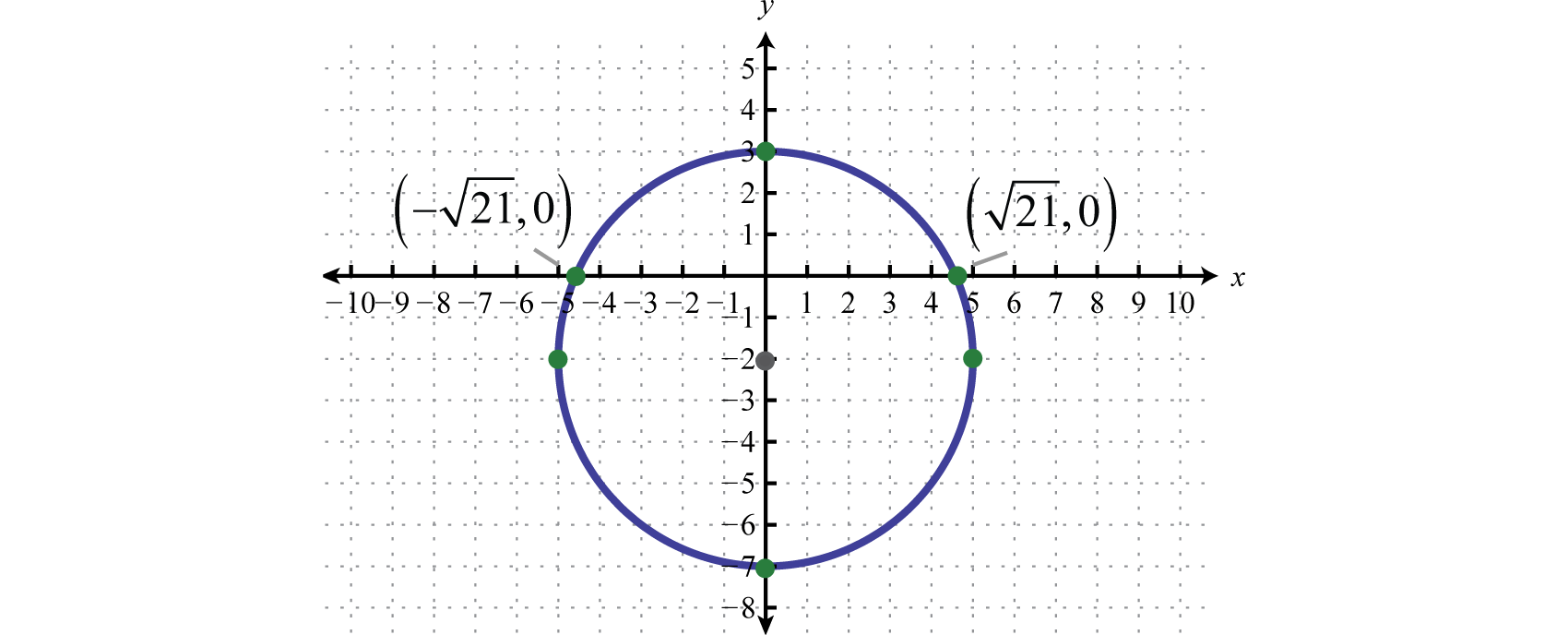
Example four
Graph:
Solution:
Begin past rewriting the equation in standard form.
-
Pace ane: Group the terms with the same variables and move the abiding to the right side. In this case, subtract 13 on both sides and grouping the terms involving 10 and the terms involving y as follows.
-
Step 2: Complete the square for each group. The idea is to add the value that completes the foursquare, , to both sides for both groupings, and so cistron. For the terms involving ten use and for the terms involving y use
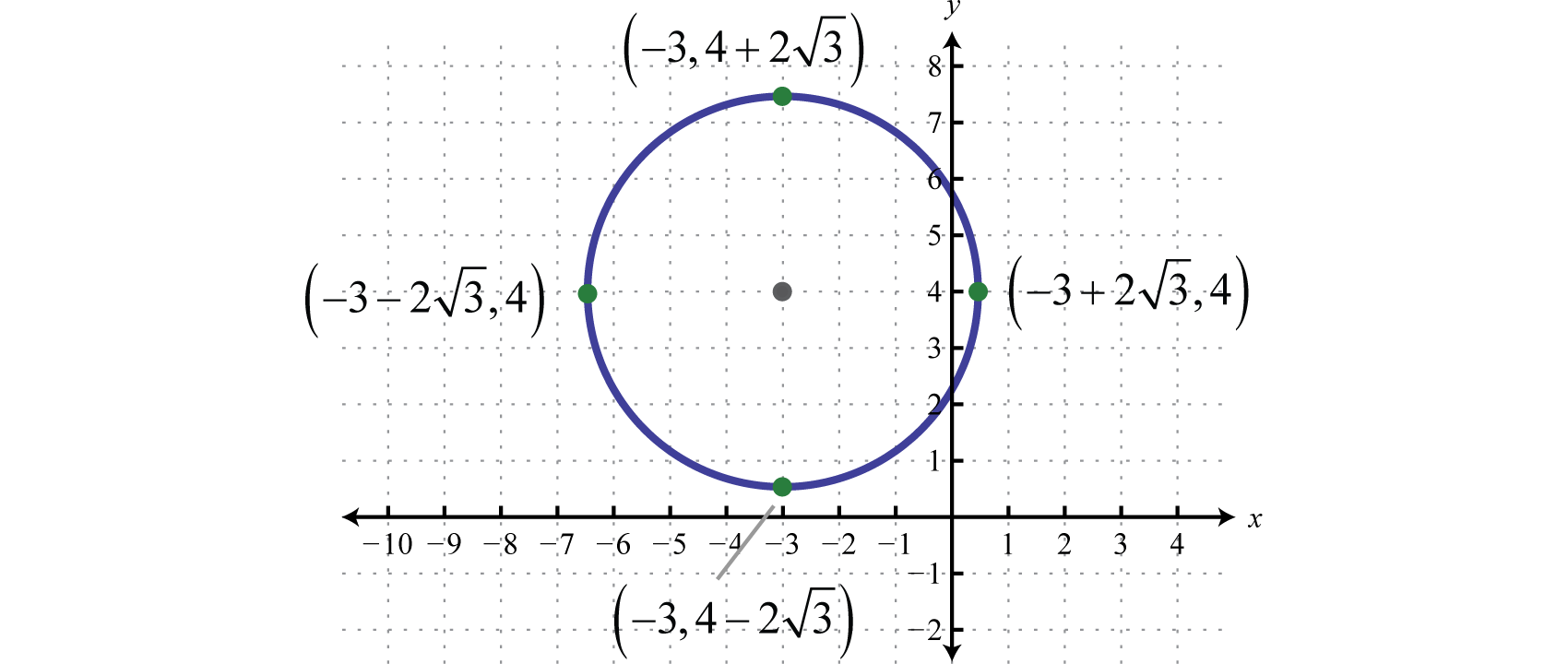
- Step three: Make up one's mind the heart and radius from the equation in standard form. In this case, the centre is and the radius
- Step 4: From the center, mark the radius vertically and horizontally and and so sketch the circle through these points.
Answer:
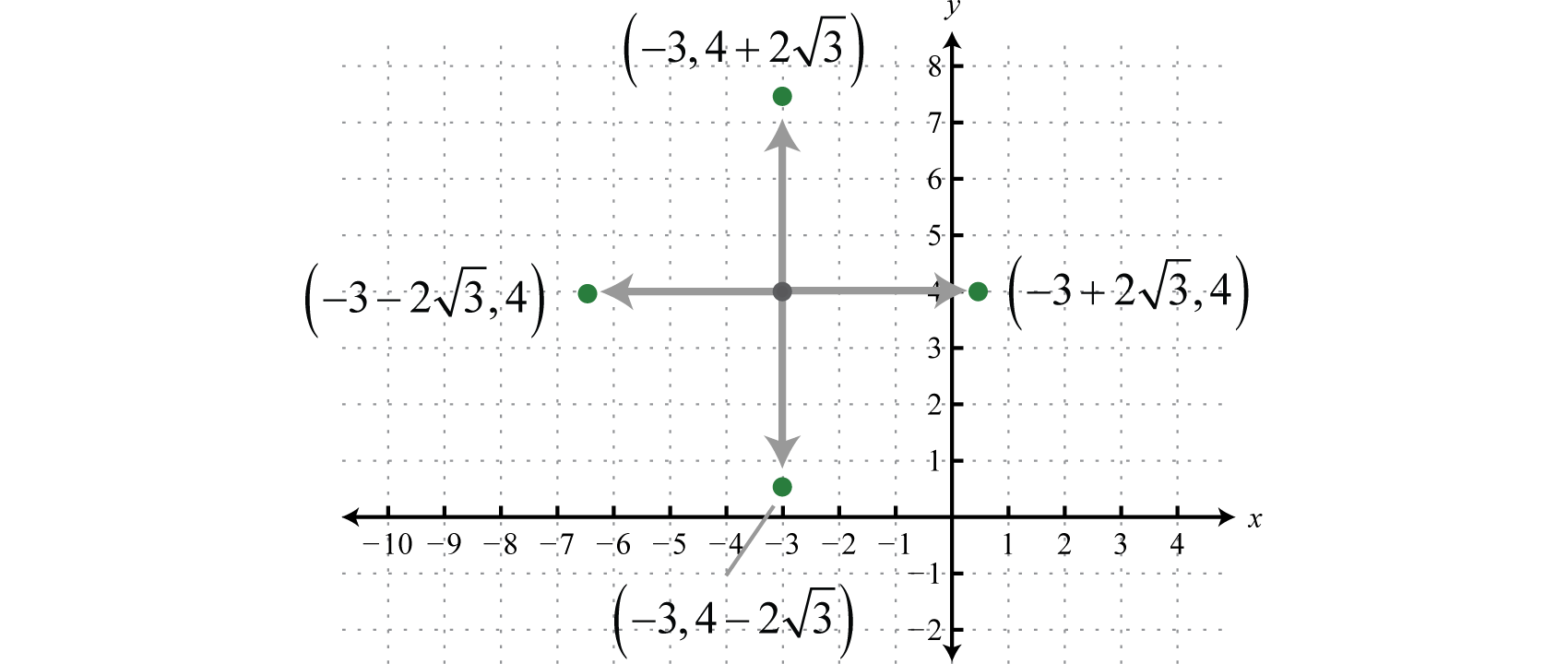
Example 5
Determine the centre and radius:
Solution:
We tin can obtain the full general form by starting time dividing both sides by 4.
Now that we have the full general form for a circumvolve, where both terms of caste two have a leading coefficient of 1, we tin use the steps for rewriting information technology in standard form. Begin by adding to both sides and group variables that are the aforementioned.
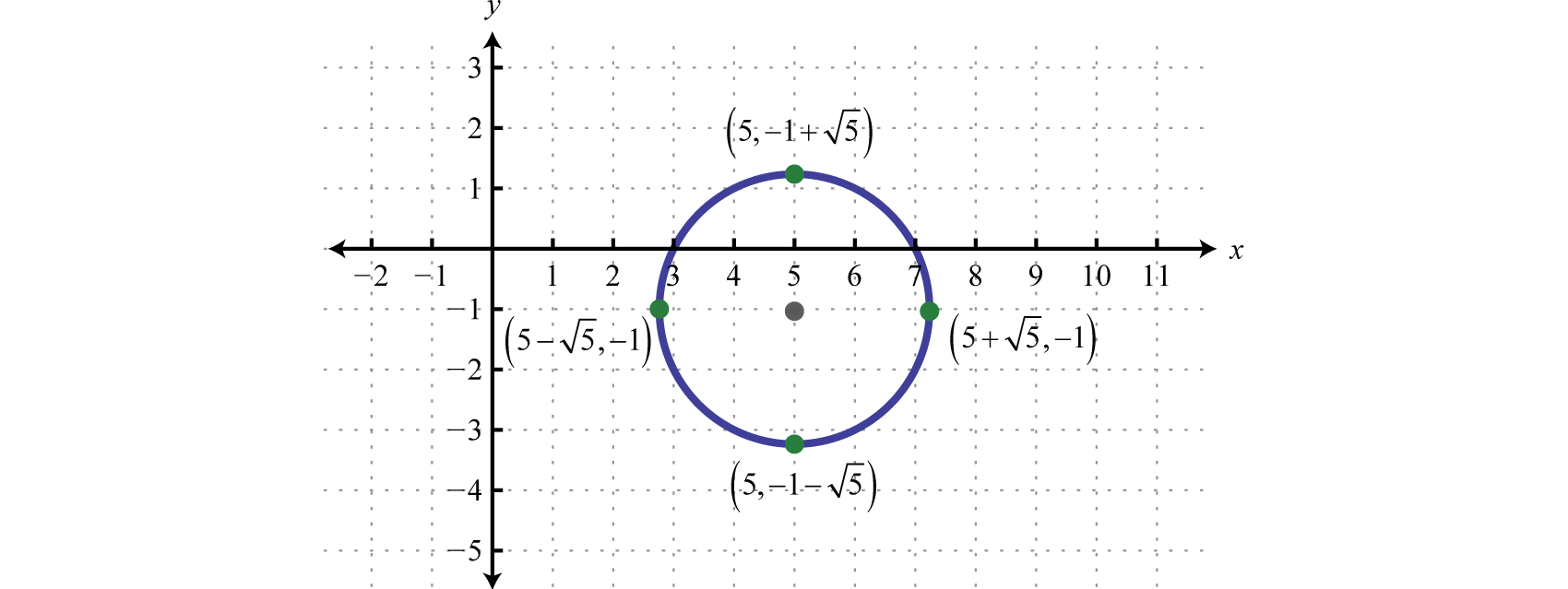
Next complete the square for both groupings. Utilize for the first group and for the 2nd grouping.
Respond: Middle: ; radius:
In summary, to convert from standard form to general class we multiply, and to convert from full general form to standard class we consummate the foursquare.

Try this! Graph:
Reply:
Central Takeaways
- The graph of a circle is completely adamant past its centre and radius.
- Standard form for the equation of a circle is The center is and the radius measures r units.
- To graph a circle mark points r units up, downward, left, and right from the center. Draw a circle through these four points.
- If the equation of a circle is given in general course , group the terms with the same variables, and complete the square for both groupings. This will result in standard form, from which nosotros can read the circle'due south center and radius.
- We recognize the equation of a circle if it is quadratic in both 10 and y where the coefficient of the squared terms are the same.
Topic Exercises
-
-
-
-
-
-
-
Middle with radius
-
Middle with radius
-
Eye with radius
-
Center with radius
-
Middle with radius
-
Center with radius
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
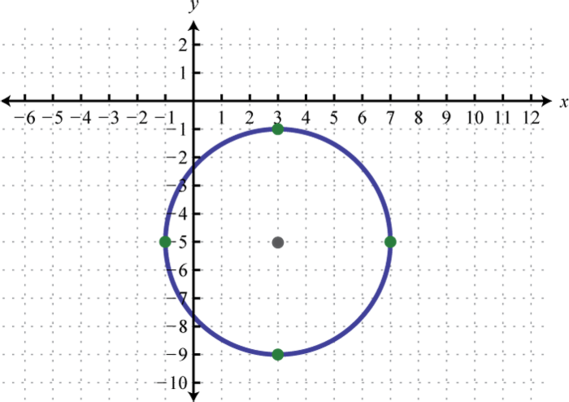
Circle with center passing through
-
Circumvolve with center passing through
-
Circumvolve whose diameter is defined by and
-
Circle whose diameter is defined by and
-
Circumvolve with heart and area square units.
-
Circle with middle and circumference square units.
-
Discover the surface area of the circumvolve with equation
-
Notice the circumference of the circle with equation
Part A: The Circle in Standard Form
Determine the center and radius given the equation of a circle in standard class.
Determine the standard form for the equation of the circle given its center and radius.
Graph.
Find the x- and y-intercepts.
Find the equation of the circle.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Determine the area of the circle whose equation is
-
Make up one's mind the area of the circle whose equation is
-
Determine the circumference of a circumvolve whose equation is
-
Make up one's mind the circumference of a circumvolve whose equation is
-
Find general form of the equation of a circle centered at passing through
-
Find full general form of the equation of a circle centered at passing through
-
-

-
-

Part B: The Circle in General Form
Rewrite in standard class and graph.
Given a circle in general course, determine the intercepts.
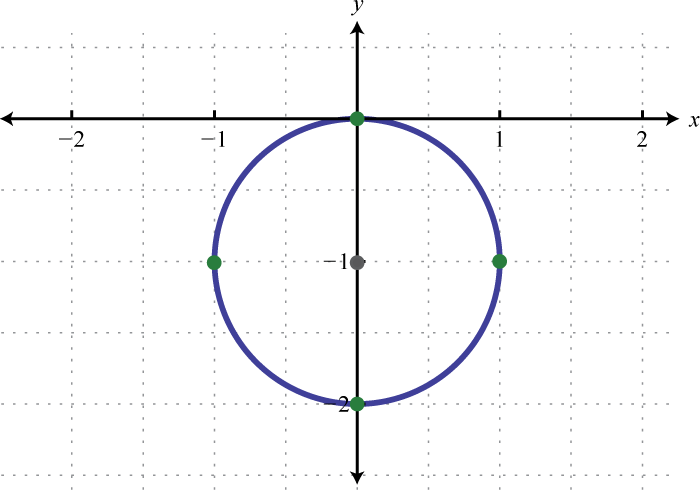
Given the graph of a circumvolve, determine its equation in general form.
-
Is the middle of a circle office of the graph? Explain.
-
Make upwardly your own circle, write it in full general grade, and graph it.
-
Explicate how we can tell the deviation between the equation of a parabola in full general course and the equation of a circle in full general form. Requite an instance.
-
Practice all circles have intercepts? What are the possible numbers of intercepts? Illustrate your explanation with graphs.
Function C: Discussion Board
Answers
-
Center: ; radius:
-
Center: ; radius:
-
Center: ; radius:
-
-
-
-
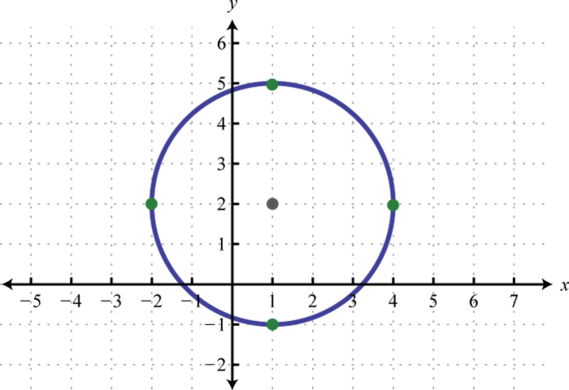
-

-

-

-

-

-
x-intercepts: ; y-intercepts:
-
x-intercepts: none; y-intercepts: ,
-
x-intercepts: ; y-intercepts:
-
x-intercepts: none; y-intercepts: none
-
-
-
-
square units
-
;
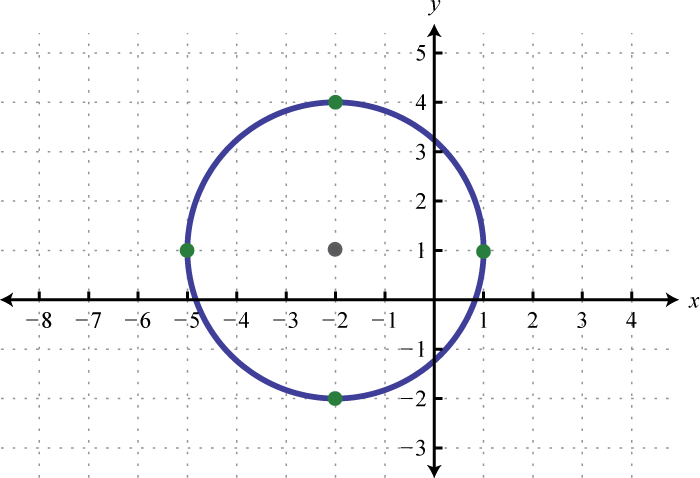
-
;

-
;
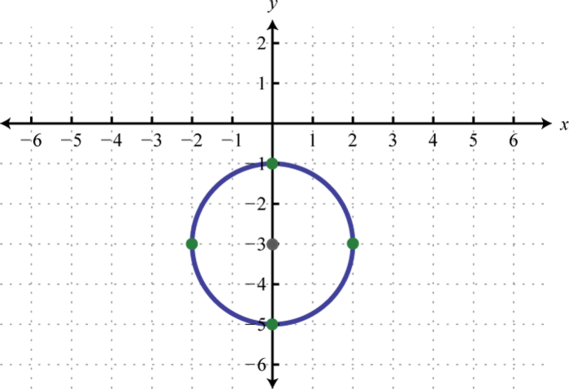
-
;
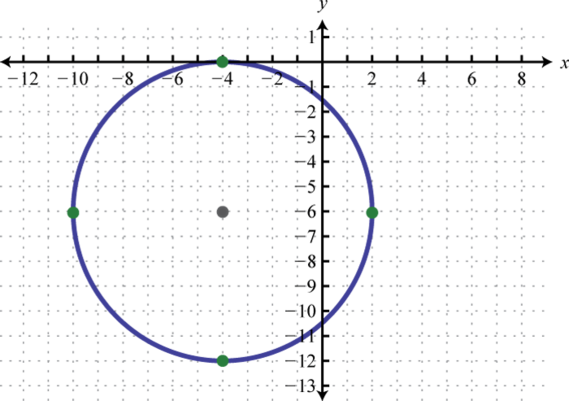
-
;
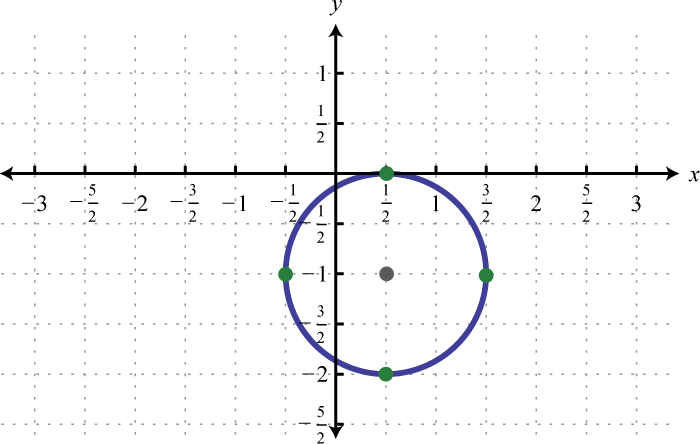
-
;
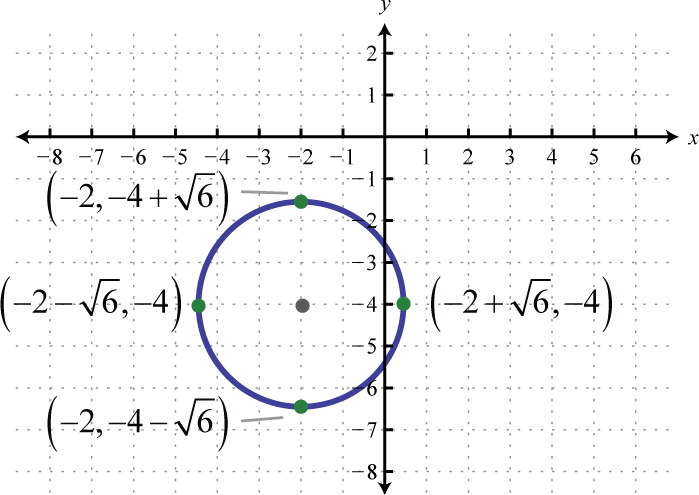
-
;
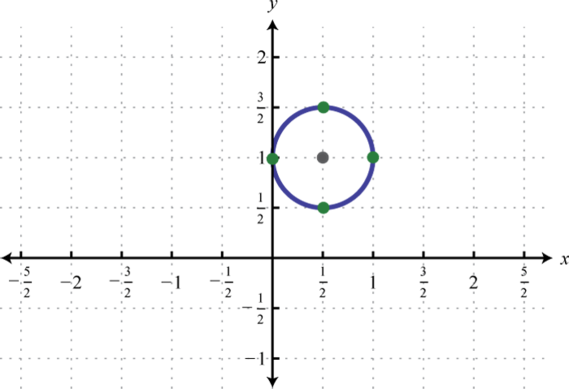
-
;
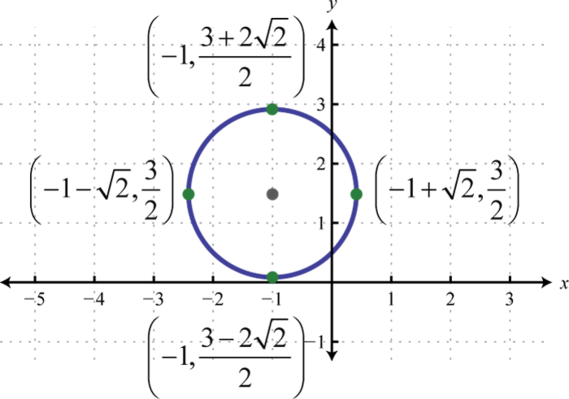
-
;
-
10-intercepts: , ; y-intercepts: none
-
10-intercepts: ; y-intercepts: ,
-
x-intercepts: , ; y-intercepts:
-
foursquare units
-
units
-
-
-
-
Answer may vary
-
Respond may vary
Source: https://saylordotorg.github.io/text_intermediate-algebra/s11-02-circles.html
Belum ada Komentar untuk "Draw Circle Given Center and Radius"
Posting Komentar